Basic equations
There are are two basic equations, for dealing with tracks in a detector :
- conservation of four-momenta : p1 + p2 +... = p'1+ p'2 + ... (1)
(considering initial particles of four momenta p1, p2..., and final particles of momenta p'1, p'2....).
- Special Relativity Kinetic Energy Relation : E2 = p2 + m2 (2)
(For any real particle with four momentum p, energy E and mass m. Here we use natural unit c=1, otherwise you change p to pc and m to mc2).
For example, if a neutral particle decays in two charged particles (the neutral particle is not seen in a bubble chamber or wires chambers), the momentum of the neutral particle can be calculated by adding the momenta of the two charged ones, (1), and then the mass of the neutral by (2). Let's take the example of of a neutral kaon decaying in two charged pions : K0(p) -- > pi+(p1) + pi+(p2) :
px = p1x + p2x , py = p1y + p2y , pz = p1z + p2z, E = E1 + E2 then m = Sqrt(E2 -px2 - py2 -pz2)
Reminds you that a four-momentum vector has four components p(px, py, pz, E) and that conservation law gives in fact four relations :
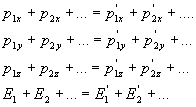
So Kinetic Energy Relation writes : E2 = px2 + py2 + pz2 + m2. By bold p in the above kinetic energy relation, we mean the spatial vector, px, py, pz. Non bold "p" is space-time vector p(p, E).
To this two basic equations, a third can be added, for real on-shell particle :
p2 = m2 and, for a massless particle, p2 = 0 (3)
p2 is in this case the scalar product p.p, in space-time four components space.
This scalar product of two four vectors p1 and p2 can be defined by the following relation ::
p1.p2
= E1E2 - p1xp2x - p1yp2y
- p1zp2z.
It differs from ordinary scalar product by the minus sign between time and spatial components. The so called "metric signature", (+1,-1,-1,-1), with c=1, is used here. This is the most common in particle physics. You can also encounter p1.p2 = p1x.p2x + p1yp2y + p1zp2z - E1E2. In this case the "signature" (+1, +1, +1, -1) is employed, related to four vector being written in the form (x, y, z, ict).
For a single real particle (on mass-shell), we can verify that:
p2 = E2 - p2 = p2 + m2 - p2 = m2
The scalar product is invariant, so this relation holds in any frame (Center of Mass, C.M, frame, Lab frame...).